Sistema de Ecuaciones 3x3

 Un sistema 3x3 significa 3 ecuaciones con 3 incógnitas.

Al igual que cuando resuelves sistemas de dos ecuaciones, hay tres posibles resultados para la solución de un sistema de tres variables. Pueden suceder tres casos cuando resolvemos sistemas 3x3: 

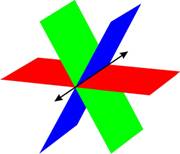
Existe una solución: Para que tres ecuaciones con tres variables tengan una solución, los planos deben interesectarse en un sólo punto.

 

 

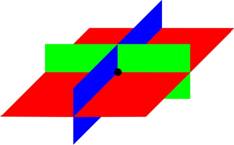
No hay solución: Los tres planos no tienen ningún punto en común. (Observa que dos ecuaciones podrían tener puntos en común una con la otra, pero no con las tres.) Abajo hay ejemplos de algunas maneras que esto sucede.

 

    

 

Existe un número infinito de soluciones: Esto ocurre cuando los tres planos se intersectan en una recta. Y también puede ocurrir cuando los tres planos están en el mismo plano.

 

     

Métodos Para Resolver los Sistemas de Ecuaciones 3x3

Sustitución: 

Este método consiste en despejar alguna de las incógnitas en una ecuación (de preferencia la incógnita que tenga  menor coeficiente) y sustituir su valor en las otras dos ecuaciones.

Ejercicio resuelto:

1) Despejamos una de las variables:

2) Sustituimos la variable en las ecuaciones restantes:

 

3) Se resuelve como si fuera un sistema de ecuaciones 2x2. Despejar cualquiera de las variables de las dos ecuaciones: 

4) Reemplazar la variable:

5) Reemplazamos el valor encontrado:

6) Reemplazamos las dos variables encontradas en la 2da ecuación, para encontrar la última variable:

7) Comprobamos:

Video explicativo:

Igualación: 

Consiste en despejar la misma incógnita de dos ecuaciones e igualarlas, para obtener el valor de la segunda incógnita y después sustituirlo en cualquiera de las ecuaciones.

Ejercicio resuelto:

             1) Despejamos la misma variable en las 3 ecuaciones:

    

2) Igualamos las dos primeras ecuaciones:

3) Igualamos la 2da ecuación con la 3ra:

4) Reemplazamos en la primera ecuación los valores encontrados: 

5) Comprobamos:

Video explicativo:

Reducción:

Tomamos dos ecuaciones cualesquiera y eliminamos una incógnita, resultando una ecuación de 2 incógnitas, ahora tomamos la que queda con una cualquiera de las dos tomadas anteriormente y eliminamos la misma incógnita que en el caso anterior, resultando otra ecuación de 2 incógnitas. De esta forma tenemos un sistema de ecuaciones 2x2.

Ejercicio resuelto: 

1) Tomamos la 1ra y 3ra ecuación y eliminamos la incógnita “z” :  

2) Tomamos la 2da y 3ra ecuación y eliminamos la misma incógnita:  

3)  Tenemos un sistema de ecuaciones 2x2, eliminamos la incógnita “y” :    

  

4) Reemplazamos el valor de “x” en la 5ta ecuación  y encontramos el valor de “y”:  

5) Reemplazamos las variables encontradas en la 1ra ecuación para encontrar el valor de “z”:  

6) Comprobamos:

Video explicativo:

Referencia:

Resolviendo Sistemas de Tres Variables. (s. f.). Montereyinstitute. https://www.montereyinstitute.org/courses/DevelopmentalMath/TEXTGROUP-9-14_RESOURCE/U14_L3_T1_text_final_es.html